Определение двудольного графа

Двудольный граф - граф, вершины которого можно разбить на два множества так, что каждое ребро соединяет вершины из разных множеств.

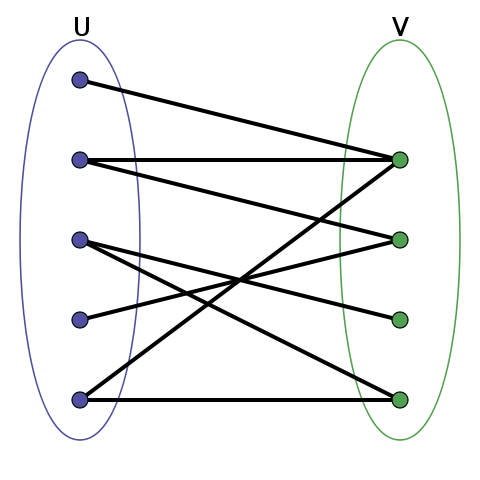
Двудольный граф

Часто в контексте двудольных графов используется понятие цвета вершины. Разбитие графа на две доли называется покраской его вершин в два различных цвета. Каждое ребро должно соединять вершины различного цвета.

Граф с вершинами покрашенными двумя цветами

Существует ещё один признак двудольности графа: граф является двудольным тогда и только тогда, когда в нём отсутствуют циклы нечётной длины.

Проверка графа на двудольность

Для проверки графа на двудольность и разбития его на доли чаще всего используется DFS.

Начинаем покраску с произвольной вершины, которую красим в произвольный цвет. При прохождении по каждому ребру красим следующую вершину в противоположный цвет. Если при переборе соседних вершин мы нашли вершину, уже покрашенную в тот же цвет, что и текущая, то в графе существует нечётный цикл, а значит, он не является двудольным.

Реализация

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#include <bits/stdc++.h>

using namespace std;

vector<int> graph[100000];
char color[100000];     //Цвет будем представлять типом char
                        //0 - вершина ещё не покрашена; 1, 2 - различные цвета.

inline char invert(int c) {
    return c == 1 ? 2 : 1;
}

void dfs(int v, char c) {   //c - цвет текущей вершины
    color[v] = c;

    for (int u: graph[v]) {
        if (color[u] == 0) {    //непосещённая вершина
            dfs(u, invert(c));
        } else if (color[u] == c) {
            cout << "Graph is not bipartite." << endl;
            exit(0);
        }
    }
}

int main() {
    //Ввод графа...

    //Двудольный граф может быть несвязным (тогда существуют несколько способов покраски).
    for (int i = 0; i < n; i++) {
        if (color[i] == 0) {
            dfs(i, 1);
        }
    }

    cout << "Graph is bipartite." << endl;
}

Хроматическое число графа

Определение двудольных графов обобщается на произвольное количество цветов. Хроматическим числом графа называется минимальное количество цветов, в которые можно покрасить его вершины так, чтобы каждое ребро соединяло вершины различного цвета. Хроматическое число двудольных графов равно \(2\), а хроматическое число графа, изображённого ниже, равно \(3\).

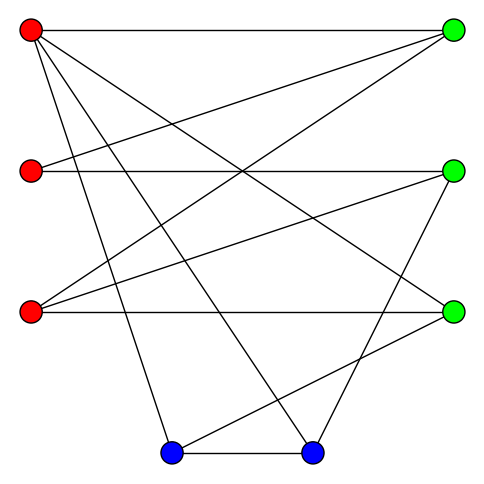
Граф, покрашенный тремя цветами

Задача проверки возможности покраски графа \(k\) цветами при \(k \ge 3\) не имеет эффективного (полиномиального) решения. Единственным доказанным решением является полный перебор всех покрасок за \(O(k^N)\). Эта задача является классической NP-полной (не имеющей полиномиального решения) задачей.