Поиск компонент связности
Определение компоненты связности
Понятие компоненты связности вытекает из понятия связности графа. Попросту говоря, компонента связности - часть графа (подграф), являющаяся связной. Формально, компонента связности - набор вершин графа, между любой парой которых существует путь.
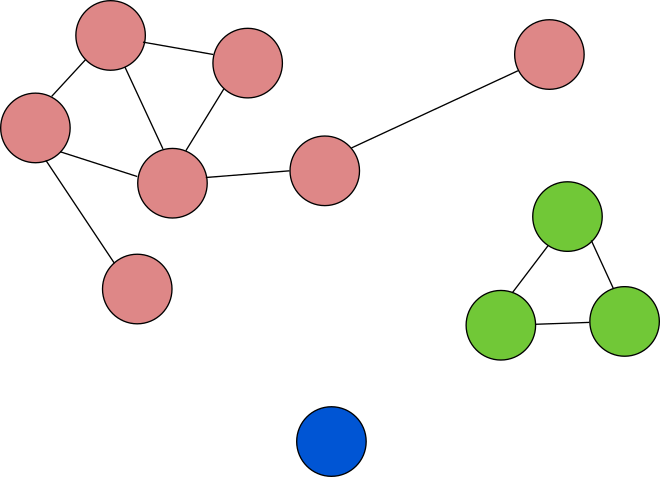
Граф на иллюстрации содержит три компоненты связности, закрашенные разными цветами. Можно заметить, что даже одна вершина, изолированная от остального графа, составляет компоненту связности.
Общее понятие связности распространяется только на неориентированные графы. Для описания ориентированных графов используются понятия сильной и слабой связности, но они выходят за границы материала этой лекции.
Алгоритм поиска компонент связности
Для поиска компонент связности используется обычный DFS практически без модификаций (можно использовать и BFS). При запуске обхода из одной вершины, он гарантированно посетит все вершины, до которых возможно добраться, то есть, всю компоненту связности, к которой принадлежит начальная вершина. Для нахождения всех компонент просто попытаемся запустить обход из каждой вершины по очереди, если мы ещё не обошли её компоненту ранее.
Реализация
Приведём два варианта реализации с разным способом хранения компонент связности.
Простейший вариант: просто заполнить массив \(comp\), где \(comp[i]\) - номер компоненты связности, к которой принадлежит вершина \(i\).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;
vector<int> graph[100000];
bool used[100000];
int comp[100000];
void dfs(int v, int c_num) { //c_num - номер текущей компоненты связности.
used[v] = true;
comp[v] = c_num;
for (int u: graph[v]) {
if (!used[u]) {
dfs(u, c_num);
}
}
}
int main() {
//Ввод графа...
int c_num = 1; //Номер очередной компоненты.
//Нумеровать можно как с 0, так и с 1, как вам удобнее.
for (int i = 0; i < n; i++) {
if (!used[i]) { //если мы ещё не посетили эту вершину, обходя одну из предыдущих
dfs(i, c_num);
c_num++;
}
}
for (int i = 0; i < n; i++) {
cout << "Vertex " << i + 1 << " belongs to component " << comp[i] << endl;
}
}
Другой вариант: явно хранить для каждой компоненты вектор из вершин, входящих в неё. Компоненты (векторы) хранить в векторе (из векторов).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
using namespace std;
vector<int> graph[100000];
bool used[100000];
vector<vector<int>> comps;
void dfs(int v) { //информацию о компоненте в DFS больше передавать не нужно,
//он просто будет добавлять вершины в последний вектор в comps.
used[v] = true;
comps.back().push_back(v);
for (int u: graph[v]) {
if (!used[u]) {
dfs(u);
}
}
}
int main() {
//Ввод графа...
for (int i = 0; i < n; i++) {
if (!used[i]) {
comps.push_back(vector<int>()); //добавляем в comps новый пустой вектор,
//в который DFS будет записывать посещённые вершины.
dfs(i);
}
}
for (vector<int>& comp: comps) {
cout << "Component: ";
for (int v: comp) {
cout << v + 1 << ", ";
}
cout << endl;
}
}