Взвешенные графы. Алгоритм Дейкстры
Взвешенные графы
В классических графах все рёбра считаются равноценными и длина пути соответствует количеству рёбер, которые он содержит. Однако часто в задаче каждому ребру соответствует некоторый параметр - длина ребра или стоимость прохождения по нему. В терминологии графов такой параметр называется весом ребра, а граф, содержащий взвешенные рёбра, взвешенным.
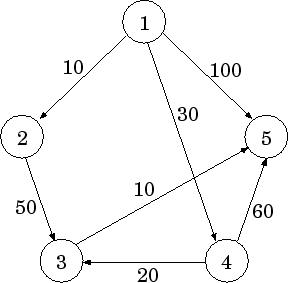
Типичная задача для таких графов - поиск кратчайшего пути. Например, в этом графе кратчайший путь между вершинами \(1\) и \(5\): \(1 - 4 - 3 - 5\), так как его вес равен \(30 + 20 + 10 = 60\), а вес ребра \(1 - 5\) равен \(100\).
Алгоритм Дейкстры
Классический алгоритм для поиска кратчайших путей во взвешенном графе - алгоритм Дейкстры (по имени автора Эдгара Дейкстры). Он позволяет найти кратчайший путь от одной вершины графа до всех остальных за \(O(M \log N)\) (\(N, M\) - количество вершин и рёбер соответственно).
Принцип работы алгоритма напоминает принцип работы BFS: на каждом шаге обрабатывается ближайшая ещё не обработанная вершина (расстояние до неё уже известно). При её обработке все ещё не посещённые соседи добавляются в очередь для посещения (расстояние до каждой из них рассчитывается как расстояние до текущей вершины + длина ребра). Главное отличие от BFS заключается в том, что вместо классической очереди используется очередь с приоритетом. Она позволяет нам выбирать ближайшую вершину за \(O(\log N)\).
Анимация выполнения алгоритма Дейкстры для поиска кратчайшего пути из вершины \(a\) в вершину \(b\):
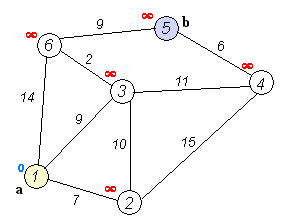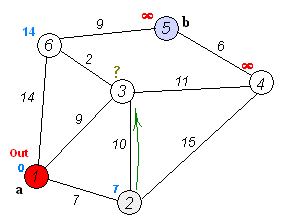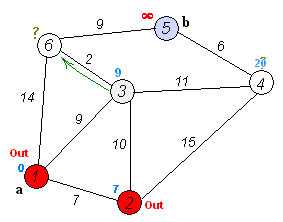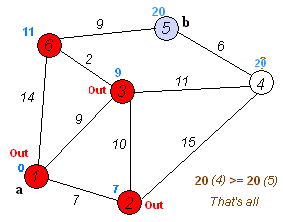
С помощью псевдокода алгоритм Дейкстры описывается следующим образом:
ans = массив расстояний от начальной вершины до каждой.
изначально заполнен бесконечностями (ещё не достигнута).
ans[start] = 0
q = очередь с приоритетом, хранящая пары (v, dst),
где dst - предполагаемое расстояние до v
добавить (start, 0) в q
пока q не пуста:
(v, dst) = первая вершина в очереди (с минимальным расстоянием), и расстояние до неё
извлечь (v, dst) из очереди
если ans[v] < dst: //мы уже обработали эту вершину, используя другой путь
перейти к следующей вершине
для каждой v -> u:
n_dst = dst + len(v -> u) //расстояние до u при прохождении через v
если n_dst < ans[u]: //если мы можем улучшить ответ
ans[u] = n_dst
добавить (u, n_dst) в q
Как видите, в очереди с приоритетом хранится не только номер вершины, но и вычисленное расстояние до неё, по которому и ведётся сортировка. Также возможна ситуация, при которой одна и та же вершина будет помещена в очередь несколько раз с разным расстоянием (так как она достижима по нескольким рёбрам). В такой ситуации обрабатываем её только один раз (с минимальным возможным расстоянием).
Реализация
В нашей очереди с приоритетом должны храниться пары (вершина, расстояние до неё),
причём отсортированы они должны быть по уменьшению расстояния. Для этого нужно
использовать тип
std::priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>:
первым элементом пары будет расстояние, а вторым - номер вершины.
Для хранения взвешенного графа в виде списка смежности для каждой вершины мы храним вектор пар (соседняя вершина, длина ребра до неё).
Реализация на C++:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9 + 7;
vector<pair<int, int>> graph[100000];
int ans[100000];
int main() {
//Ввод графа и вершины start.
for (int i = 0; i < n; i++) {
ans[i] = INF;
}
ans[start] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
q.push({0, start});
while (!q.empty()) {
pair<int, int> c = q.top();
q.pop();
int dst = c.first, v = c.second;
if (ans[v] < dst) {
continue;
}
for (pair<int, int> e: graph[v]) {
int u = e.first, len_vu = e.second;
int n_dst = dst + len_vu;
if (n_dst < ans[u]) {
ans[u] = n_dst;
q.push({n_dst, u});
}
}
}
for (int i = 0; i < n; i++) {
cout << "Shortest path from " << start + 1 << " to " << i + 1 << " has length " << ans[i] << endl;
}
}
Реализация с восстановлением пути
Восстановление пути для алгоритма Дейкстры реализуется точно так же, как и для BFS: при успешном улучшении пути в вершину \(u\) через вершину \(v\), мы запоминаем, что \(prev[v] = u\). После окончания работы алгоритма используем массив \(prev\) для восстановления пути в обратном направлении.
Реализация на C++:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9 + 7;
vector<pair<int, int>> graph[100000];
int ans[100000];
int pr[100000]; //prev
int main() {
//Ввод графа и вершин start и end.
for (int i = 0; i < n; i++) {
ans[i] = INF;
pr[i] = -1; //Значение, обозначающее что из этой вершины возвращаться некуда
}
ans[start] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
q.push({0, start});
while (!q.empty()) {
pair<int, int> c = q.top();
q.pop();
int dst = c.first, v = c.second;
if (ans[v] < dst) {
continue;
}
for (pair<int, int> e: graph[v]) {
int u = e.first, len_vu = e.second;
int n_dst = dst + len_vu;
if (n_dst < ans[u]) {
ans[u] = n_dst;
pr[u] = v;
q.push({n_dst, u});
}
}
}
vector<int> path;
int cur = end;
path.push_back(cur);
while (pr[cur] != -1) {
cur = pr[cur];
path.push_back(cur);
}
reverse(path.begin(), path.end());
cout << "Shortest path between vertices " << start + 1 << " and " << end + 1 << " is: " << endl;
for (int v: path) {
cout << v + 1 << ", ";
}
}
Область применения алгоритма Дейкстры
Алгоритм Дейкстры является оптимальным для поиска пути практически в любых графах, но он имеет одно ограничение. Алгоритм Дейкстры неприменим для графов, содержащих рёбра с отрицательным весом. Для поиска кратчайшего пути в таких графах обычно используют алгоритм Форда-Беллмана.