Постановка задачи

Для заданного графа нужно ответить, содержит ли он хотя бы один цикл. Стоит заметить, что от нас не требуется найти все циклы, нужно всего лишь ответить, существует ли хотя бы один. Задача на поиск всех циклов решается гораздо сложнее.

Алгоритм

Для поиска цикла будем использовать DFS. Для примера разберём такой граф:

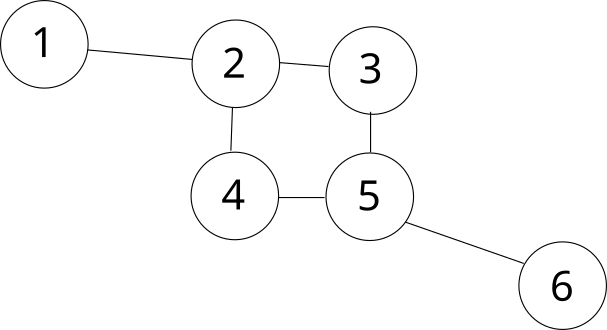
Граф с циклом

Допустим, мы запустили DFS из вершины 1, и он полностью обошёл граф. Представим обход этого графа так же, как представляем деревья, по уровням в зависимости от глубины рекурсии:

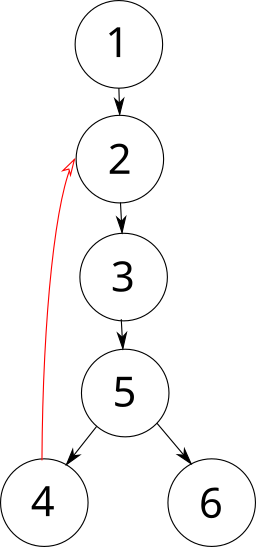
Граф с циклом с обозначенным ребром

(Примечание: это только один из возможных вариантов обхода в глубину.)

Как видите по одному из ребёр, входящих в цикл, DFS не спускался: оно выделено красным цветом. Именно по наличию таких “восходящих” рёбер в графе можно судить о наличии в нём циклов. При реализации DFS такие рёбра распознать достаточно легко: они ведут в уже посещённую (\(used\)) вершину, но не в прямого предка (\(p\)).

Реализация

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include <bits/stdc++.h>

using namespace std;

vector<int> graph[100000];
bool used[100000];

void dfs(int v, int p = -1) {    //p - прямой предок
    used[v] = true;

    for (int u: graph[v]) {
        if (!used[u]) {
            dfs(u, v);
        } else if (u != p) {
            cout << "Graph has cycles.";
            exit(0);    //Полностью выйти из программы.
        }
    }
}

int main() {
    //Ввод графа...

    //Проверяем отдельно каждую вершину, так как
    //граф может быть несвязным, но всё равно иметь циклы
    for (int i = 0; i < n; i++) {
        if (!used[i]) {
            dfs(i);
        }
    }

    //Если мы ещё не вышли не вышли из программы, в графе нет циклов.
    cout << "Graph has no cycles.";
}

Сложность: \(O(N)\)