Понятие и представление графа: матрица смежности, список смежности
Определение графа
Графы - фундаментальное понятие как в математике, так и в информатике. Проще всего объяснить его с помощью аналогии с дорожной системой. Существует определённый набор городов, некоторые из которых связаны дорогами, которые могут быть как односторонними, так и двухсторонними. Вся эта структура и называется графом.
Ну а более формально, граф - комбинация набора вершин и набора рёбер. Вершины - это города, а рёбра - дороги. Визуально граф можно представить так:
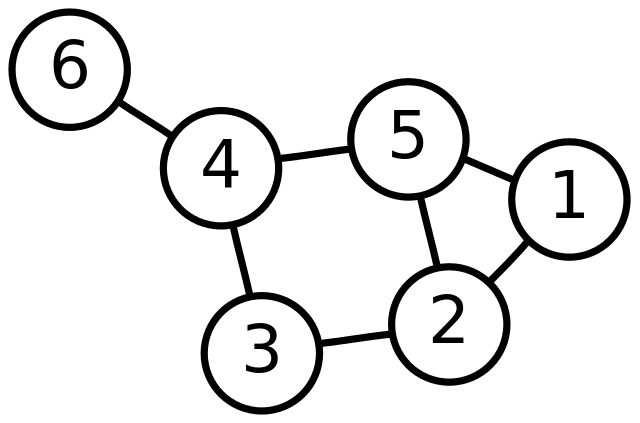
Этот граф состоит из 6 вершин, пронумерованных начиная с единицы, и 7 двухсторонних рёбер. Рёбра обычно записывают в виде пар вершин, которые они соединяют: \(1\)-\(2\), \(1\)-\(5\), \(2\)-\(3\), \(2\)-\(5\), \(3\)-\(4\), \(4\)-\(5\), \(4\)-\(6\).
Ориентированные и неориентированные графы
Мы уже упоминали, что “дороги” в графе могут быть как односторонними, так и двухсторонними. Для этого свойства существует отдельный термин: односторонние “дороги” называются ориентированными рёбрами (или дугами), а двухсторонние - неориентированными.
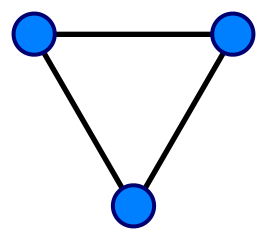
Граф, в котором все рёбра неориентированные, также называют неориентированным, а граф с ориентированными рёбрами, соответственно, ориентированным.
 |
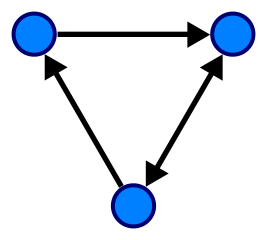 |
Слева изображён неориентированный граф, а справа - ориентированный. Как несложно догадаться, левый граф можно обходить как по часовой стрелке, так и против, а правый можно полностью обойти только по часовой, хотя одно из ребёр в нём также неориентированное (считается, что это два противоположных ориентированных ребра).
Пути и циклы
Путём в графе называется последовательность вершин, каждая из которых соединена со следующей ребром. Чаще всего под “путём” подразумевают простой путь, все вершины которого различны. Путь, который проходит через какую-либо вершину более одного раза называют сложным путём.
Если первая вершина пути совпадает с последней, то такой путь называют циклом.
Приведём примеры на этом графе:
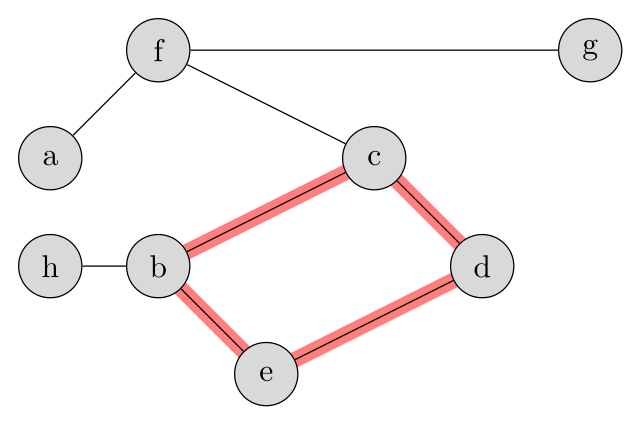
Из множества возможных простых путей самый длинный: \(a - f - c - d - e - b - h\) (существуют и другие пути с такой же длиной).
Циклом является путь \(b - c - d - e - b\) (выделен цветом). Можно начать и с любой другой вершины, например, \(c - d - e - b - c\).
Кратные рёбра и петли
Существует множество разновидностей графов, и среди них встречаются довольно специфические. В частности, так называемые мультиграфы разрешают наличие между двумя вершинами нескольких рёбер (называемых кратными рёбрами), а также наличие петель. Петля - ребро, входящее в ту же вершину, из которой исходит. Выглядят они следующим образом:
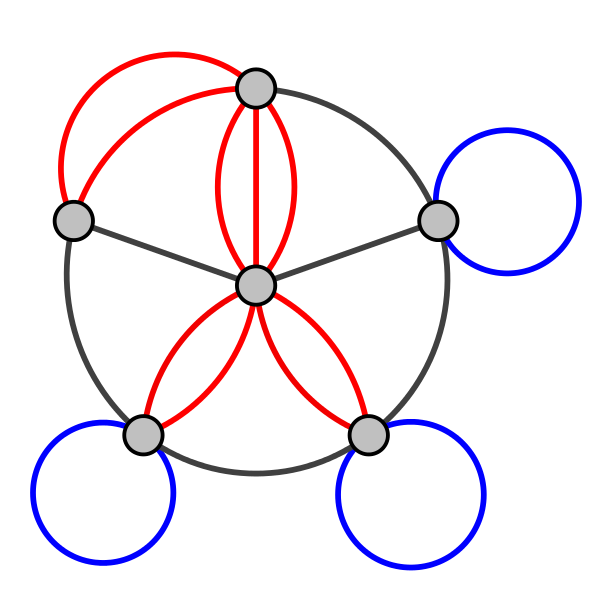
Красным выделены кратные рёбра, а синим - петли.
Мультиграфы встречаются в задачах реже чем обычные графы (называемые простыми), но всё же встречаются, поэтому стоит иметь о них элементарное представление.
Связные графы
Граф называется связным если между любой парой вершин существует хотя бы один путь. Как пример рассмотрим следующий граф:
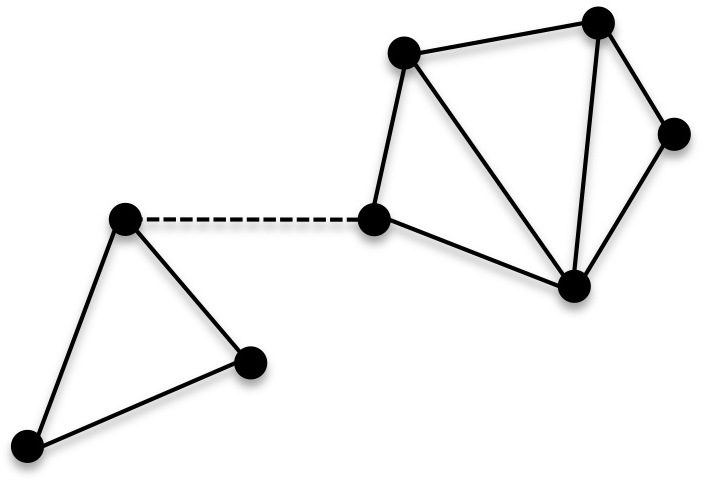
Одно из рёбер проведено штрихами. Если это ребро присутствует, то граф является связным. Если же его убрать, то связность теряется, граф разбивается на две части, друг с другом не связанные. Такие части называются компонентами связности.
Определение дерева
Дерево - вид графа, который можно назвать самым простым, но они обладают множеством особых свойств и встречаются в задачах чуть ли не чаще остальных графов.
Дерево - это связный граф без циклов, петель и кратных рёбер.
Все изображённые графы являются деревьями:
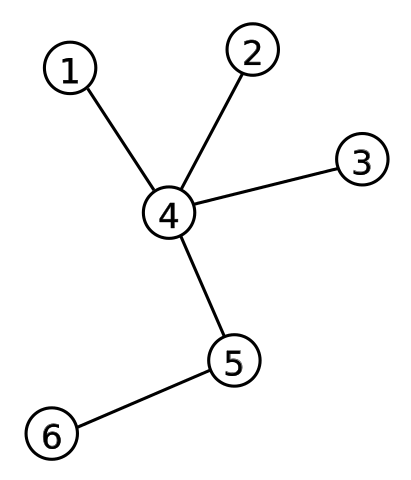
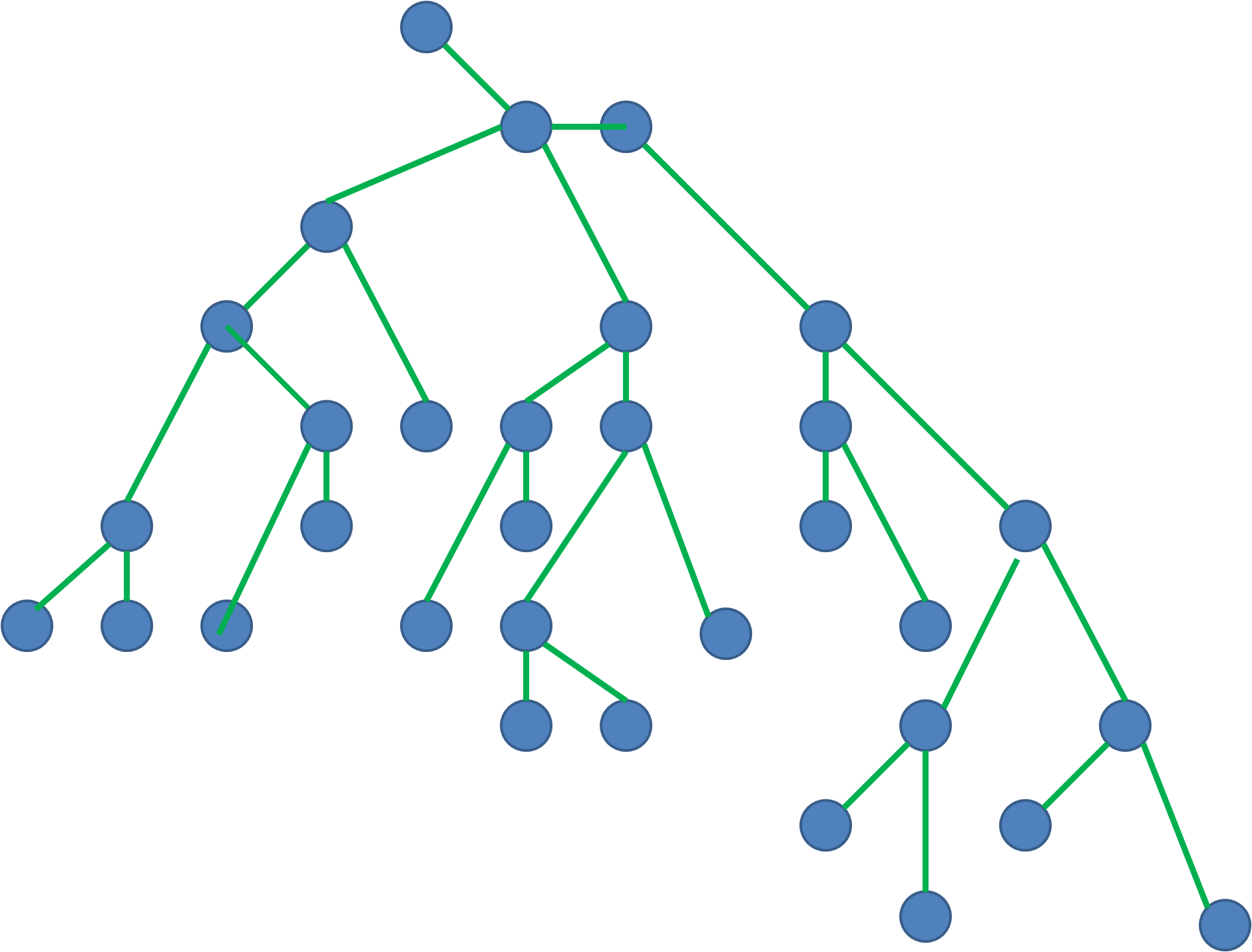
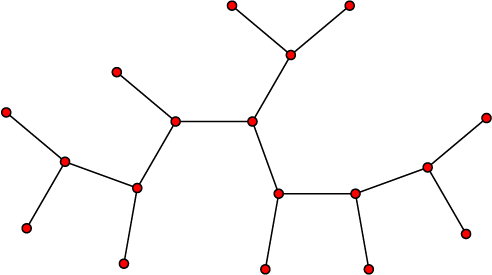
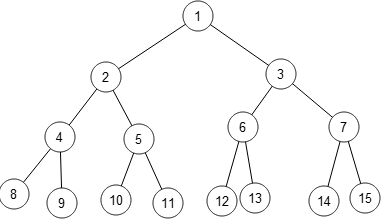
Среди множества свойств деревьев можно выделить два самых известных:
- Количество рёбер связано с количеством вершин формулой \(E = V - 1\).
- Между любой парой вершин существует ровно один путь.
Матрица смежности
Существует два основных способа представления графов в программировании.
Один из них, матрица смежности, используется гораздо реже, но очень просто
реализуется. Граф из \(N\) вершин задаётся матрицей (двумерным массивом) \(N * N\),
в которой \(g[i][j]\) - логическое значение, true или
false, обозначающее, существует ли ребро из вершины \(i\) в вершину
\(j\).
В качестве примера решим простую задачу: для каждой вершины графа выведем количество рёбер, смежных с ней.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
using namespace std;
bool graph[1000][1000];
int main() {
int n, m; //количество вершин и рёбер соответственно
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v; //номера вершин, соединённых очередным ребром
cin >> u >> v;
u--, v--; //Здесь стоит остановиться и вдуматься.
//Чаще всего в задачах вершины будут нумероваться с 1 до N,
//в отличие от индексации массивов в C++.
//У этой проблемы есть два решения.
//Первое: работать с номерами "как есть": создавать массивы размером N + 1,
//использовать циклы от 1 до N, и т.д.
//Второе: уменьшать номера вершин на единицу при вводе, и увеличивать обратно при выводе
//Какое из них использовать - ваш личный выбор.
//Для меня 1-индексация в С++ выглядит очень чужеродно, поэтому я использую второе решение.
graph[u][v] = graph[v][u] = true; //Если бы граф был ориентированным, то обратное ребро мы бы не создавали.
}
for (int i = 0; i < n; i++) {
int c = 0;
for (int j = 0; j < n; j++) {
if (graph[i][j]) {
c++;
}
}
cout << c << " edges adjacent to vertex " << i + 1 << endl;
}
}
Преимущества матрицы смежности:
- Сложность проверки наличия ребра между двумя вершинами: \(O(1)\)
Недостатки матрицы смежности:
- Занимает \(N^2\) памяти, что неприемлемо для достаточно больших графов.
- Сложность перебора всех вершин, смежных с данной: \(O(N)\)
Список смежности
Гораздо чаще для представления графов используется список смежности. Его идея заключается в хранении для каждой вершины расширяемого массива (вектора), содержащего всех её соседей.
Решим ту же задачу с использованием списка смежности (и С++11 для for-each):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
using namespace std;
vector<int> graph[100000]; //массив из 100000 векторов.
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
u--, v--;
graph[u].push_back(v);
graph[v].push_back(u);
}
for (int i = 0; i < n; i++) {
int c = 0;
for (int v: graph[i]) { //можно было бы просто записать "int c = graph[i].size();",
c++; //но такая реализация показывает, как можно перебирать
} //соседние вершины.
cout << c << " edges adjacent to vertex " << i + 1 << endl;
}
}
Если требуется также удалять рёбра, то вместо вектора нужно использовать
std::set.
Преимущества списка смежности:
- Использует \(O(M)\) памяти, что оптимально.
- Позволяет быстро перебирать соседей вершины.
- Позволяет за \(O(\log N)\) проверять наличие ребра и удалять его (при использовании
std::set).
Недостатки списка смежности:
- При работе с насыщенными графами (количество рёбер близко к \(N^2\)) скорости \(O(\log N)\) может не хватать (единственный повод использовать матрицу смежности).
- Для взвешенных графов приходится хранить
vector<pair<int, int>>, что усложняет код.