Решето Эратосфена

Определение

Решето Эратосфена - достаточно эффективный алгоритм для нахождения всех простых чисел в отрезке от \(1\) до \(N\) за \(O(N \log \log N)\).

Алгоритм достаточно тривиален: будем перебирать числа по возрастанию, начиная с \(2\), зачёркивая все числа, кратные текущему. Например, при обработке числа \(2\) будут зачёркнуты числа \(4, 6, 8, \ldots\). Если мы обнаружили незачёркнутое число, это значит, что оно простое.

Визуализация работы решета Эратосфена:

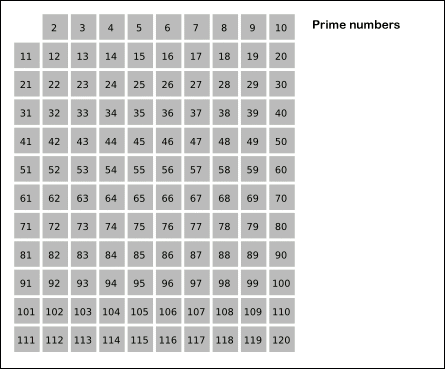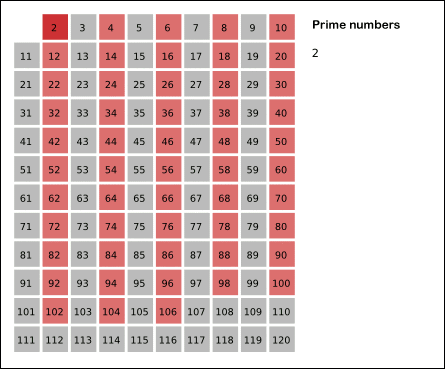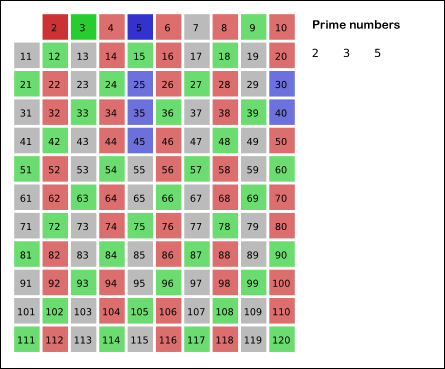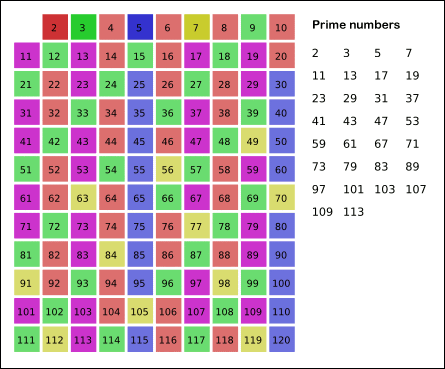
Работу решета можно значительно ускорить, если начинать зачёркивать числа, кратные \(p\), не с \(2p\), а с \(p^2\). Ведь числа \(2p, 3p, 5p, \ldots\) уже были зачёркнуты при обработке чисел \(2, 3, 5, \ldots\)

Реализация

#include <bits/stdc++.h>

using namespace std;

bool sieve[1000001];    //решето
vector<int> primes;     //вектор, в который будут добавляться простые числа

void compute_primes(int n) {
    for (int i = 2; i <= n; i++) {   //Изначально все числа не вычеркнуты.
        sieve[i] = true;
    }

    for (int i = 2; i <= n; i++) {
        if (sieve[i]) {     //если i не вычеркнуто
            primes.push_back(i);

            for (int j = i * i; j <= n; j += i) {    //вычеркиваем все кратные числа начиная с i^2
                sieve[j] = false;
            }
        }
    }
}

int main() {
    compute_primes(1000000);

    cout << "Prime numbers: ";
    for (int i: primes) {
        cout << i << ", ";
    }
}

Сложность алгоритма. Гармонический ряд

На примере решета Эратосфена можно продемонстрировать очень полезный математический факт, применяемый во многих доказательствах. А именно, имеет место следующее приближение:

\[1 + \frac{1}{2} + \frac{1}{3} + \ldots + \frac{1}{n} = \sum_{i=1}^{n} \frac{1}{i} \approx \log(n)\]

Такую сумму называют “гармоническим рядом”, и она часто появляется в оценках сложности алгоритмов. Например, посмотрим на решето Эратосфена, в самой его наивной реализации: будем выполнять зачёркивающий цикл для каждого \(x \in [2; n]\). То есть, для \(x = 2\) мы проверим \(\frac{N}{2}\) элементов (и часть из них зачеркнём), для \(x = 3\) проверим \(\frac{N}{3}\), и так далее, вплоть до \(x = N\). Напомним, что сейчас мы рассматриваем гипотетическую, самую наивную версию алгоритма, так что представим, что мы выполняем зачёркивающий цикл даже для уже зачёркнутых элементов. Заметим, что общее число итераций зачёркивающего цикла можно оценить как

\[\frac{N}{2} + \frac{N}{3} + \ldots + \frac{N}{N} = N * (\sum_{i=2}^{N} \frac{1}{i}) \approx N * (\log(N) - 1) = O(N \log N)\]

А значит сложность нашей гипотетической наивной версии алгоритма равна \(O(N \log N)\). Возвращаясь в реальность, оптимальная версия отличается от гипотетической несколькими свойствами:

• Зачёркивающий цикл выполняется только для простых \(x \le N\), а не для всех.
• Зачёркивающий цикл начинает выполнение с \(x^2\), а не с \(x\).

Используя эти свойства, можно доказать ещё более жёсткое ограничение для сложности: \(O(N \log \log N) \le O(N \log N)\), но сделать это довольно непросто. К тому же, для олимпиадных задач такая точность не всегда оправдана: например для \(N = 10^6\):

\[N \log N = 19.9 * 10^6 \\ N \log \log N = 4.3 * 10^6\]

Разница между двумя оценками достаточно небольшая, и редко помогает принять решение, достаточно ли быстрый ваш алгоритм. Впрочем, полезно всё же помнить о существовании более жёсткой оценки для решета Эратосфена, на всякий случай.