Определение

Топологическая сортировка - способ нумерации вершин ориентированного графа, при котором каждое ребро ведёт из вершины с меньшим номером в вершину с большим номером.

Для одного графа может существовать несколько спобосов топологической сортировки (например когда он несвязный), а может не существовать не одного (при наличии циклов).

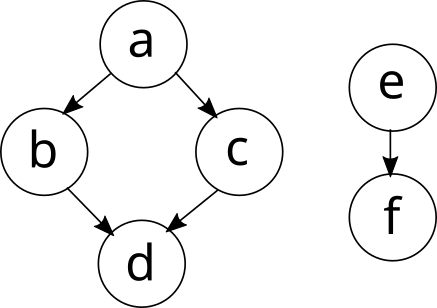
Граф из шести вершин с двумя компонентами связности

У изображённого графа существуют четыре способа топологической сортировки:

  • \(a - b - c - d - e - f\).
  • \(a - c - b - d - e - f\).
  • \(e - f - a - b - c - d\).
  • \(e - f - a - c - b - d\).

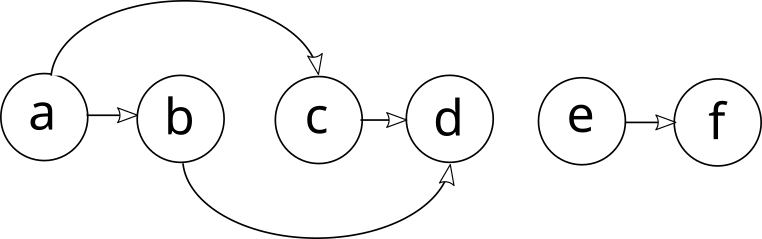
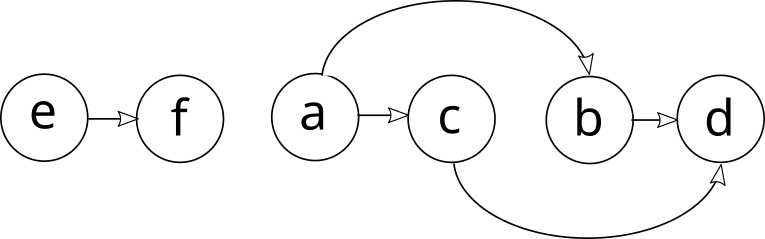
Топологическую сортировку часто изображают в виде горизонтального ряда вершин, рёбра между которыми направлены только вправо (изображены 1-й и 4-й варианты):

Топологическая сортировка графа, вариант 1 Топологическая сортировка графа, вариант 2

Алгоритм

Алгоритм топологической сортировки тривиально определяется через DFS. Будем присваивать номера в убывающем порядке: от самого большого к самому малому. Пусть мы хотим присвоить номер вершине \(v\). Будем работать в обратном порядке: сначала присвоим номера всем дочерним вершинам (рекурсивно), которые их ещё не имеют (некоторые уже могут иметь номера, так как мы могли посетить их раньше). Теперь все дочерние вершины (и, рекурсивно, все их поддеревья) уже пронумерованы. Просто присвоим следующий номер текущей вершине: он будет меньше всех номеров вершин поддерева по определению. Применяем этот алгоритм для всех вершин, ещё не посещённых ранее, по очереди.

Реализация

Вместо явного присваивания вершинам номеров, будем добавлять их в массив по мере нумерации. После окончания работы алгоритма в массиве будут содержаться все вершины в порядке убывания их номера. Просто развернём массив, и получим топологическую сортировку.

Реализация на C++:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <bits/stdc++.h>

using namespace std;

vector<int> graph[100000];
bool used[100000];
vector<int> order;    //массив для сохранения пронумерованных вершин

void dfs(int v) {
    used[v] = true;

    for (int u: graph[v]) {
        if (!used[u]) {
            dfs(u);
        }
    }

    order.push_back(v);
}

int main() {
    //Ввод графа...

    for (int i = 0; i < n; i++) {       //Нам важно, чтобы DFS посетил все вершины графа,
        if (!used[i]) {                 //а не только достижимые из нулевой. Поэтому мы явно
            dfs(i);                     //вызываем его для всех, ещё не посещённых ранее.
        }
    }

    reverse(order.begin(), order.end());

    cout << "Topological sort: ";
    for (int v: order) {
        cout << v + 1 << ", ";
    }
}

Стоит отметить, что такая реализация не проверяет возможность построения топологической сортировки. Если в графе существуют циклы, она проигнорирует их и выведет неправильный ответ. Поэтому на практике необходимо помнить о предварительной проверке графа на отстутствие циклов, если оно не гарантируется в задаче.