Битовые маски. Динамическое программирование по маскам

Битовые маски

Как известно, числа в памяти компьютера представляются в двоичной системе счисления в виде последовательности битов. Один бит может иметь значение \(0\) или \(1\). Можно провести аналогию между битами и значениями типа bool: \(0\) обозначает false, а \(1\) - true. По такой аналогии число (последовательность битов) можно представить как массив значений bool. Например, тип int может обозначать массив из \(32\) значений bool, а long long - из \(64\).

Чаще всего массивы bool небольшого размера испольуются для обозначения некоторого подмножества объектов, выбранного из множества. Например, для обозначения элементов с индексами \(1\) и \(4\) (0-индексация), выбранных из множества из пяти элементов используется массив \(\{false, true, false, false, true\}\), или \(\{0, 1, 0, 0, 1\}\). Его можно представить в виде значения типа int: \(10010_2\) (индексация обычно начинается с младших битов числа, записываемых справа).

При интерпретации такого значения как обычного числа, оно будет равно \(10010_2 = 18_{10}\). Но при интерпретации его как массива логических значений (битов), оно будет обозначать \(\{0, 1, 0, 0, 1\}\). С точки зрения C++ эти два значения равносильны, и то, является ли значение типа int числом, или массивом bool, зависит только от контекста, в котором оно используется.

При использовании значений типа int или long long как массивов из bool, такие значения называются битовыми масками.

Операции с битовыми масками

Для работы с масками используются побитовые операции \(and, or, xor\), и битовые сдвиги.

Пусть две маски обозначают два множества элементов, и нам нужно получить маску, содержащую элементы, входящие в оба множества (пересечение множеств). В новой маске true должны находится только в тех позициях, где в обеих масках находились true. Несложно заметить, что такое описание соответствует побитовой операции \(and\):

int c = a & b; // маска c равна пересечению масок a и b

Другой распространённой операцией является объединение множеств. При объединении в новой маске true должны находиться в тех позициях, в которых в хотя бы одной из масок находилось true. Такое описание соответствует побитовой операции \(or\):

int c = a | b; // маска c равна объединению масок a и b

Для получения значения индивидуального бита используется комбинация битового сдвига вправо и операции \(and\). Сначала нам нужно сдвинуть биты маски так, чтобы нужный бит оказался самым младшим (находился справа). Затем нам нужно откинуть все остальные биты маски. Реализуется это следующим образом:

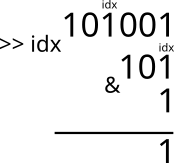
int bit = (a >> idx) & 1; // bit равен значению idx-го бита в маске a

Для установки значения определённого бита маски в true мы должны применить к нему операцию \(or\ true\). Реализуется это так (ко всем остальным битам применяется \(or\ false\), не имеющая никакого эффекта):

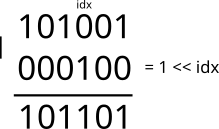
int b = a | (1 << idx); // маска b - копия маски a, в которой idx-ый бит установлен в true

Для изменения значения определённого бита на противоположное, нужно применить к нему операцию \(xor\ true\). Ко всем остальным битам применяется \(xor\ false\), также не имеющая никакого эффекта:

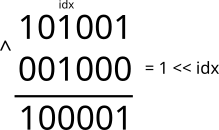
int b = a ^ (1 << idx); // маска b - копия маски a с противоположным значением idx-го бита

Это самые распространённые операции, выполняемые с масками. Существует множество других, здесь не приведённых, но все они основаны на \(and, or, xor\), и сдвигах.

Динамическое программирование по подмножествам

Битовые маски часто используются как параметры для динамического программирования. Такой вид ДП называется ДП по маскам, или ДП по подмножествам.

Классической задачей на ДП по подмножествам является широко известная задача о коммивояжёре (англ. TSP - Travelling Salesman Problem). В общем виде она ставится следующим образом:

Существует \(N\) городов, между некоторыми из которых есть дороги. Требуется обойти все города, вернувшись в первый, так, чтобы длина пути была минимальной.

Эта задача является классической NP-полной задачей, и ДП по подмножествам со сложностью порядка \(O(2^N * N^2)\) - её оптимальное решение.

Для простоты реализации примем, что города являются точками на геометрической плоскости, и между каждой парой есть путь, длина которого равна расстоянию между точками.

Обозначим за \(dp[mask][i]\) - длину кратчайшего пути, начинающегося в вершине \(0\), проходящего через все вершины \(mask\), и заканчивающегося в вершине \(i\) (\(0 \in mask; i \in mask\)). Начальные значения ДП можно записать следующим образом:

\[dp[mask][i] = \infty \\ dp[\{0\}][0] = 0\]

Запись \(\{0\}\) обозначает маску, обозначающую множество, состоящее только из элемента \(0\).

Формула перехода для ДП выглядит так:

\[dp[mask][i] = \min_{\substack{j\ \in\ mask \backslash i}} (dp[mask \backslash i][j] + dst(j, i))\]

Запись \(mask \backslash i\) обозначает множество \(mask\) без элемента \(i\).

Формула перехода обозначает следующее: чтобы попасть в вершину \(i\), нужно перейти в неё из какой-либо другой вершины \(j\), также входящей в \(mask\). Из всех таких вершин нужно выбрать такую, что общая длина пути в \(i\) будет наименьшей. Общая длина пути рассчитывается как длина пути в \(j\) (\(dp[mask \backslash i][j]\)) плюс длина пути из \(j\) в \(i\) (\(dst(j, i)\)).

Чтобы найти минимальную длину цикла из всех вершин, нужно перебрать вершину \(i\), и выбрать такую, что длина цикла \(0 - \ldots - i - 0\) минимальна. Длина такого цикла вычисляется по формуле \(dp[\mathbb{V}][i] + dst(i, 0)\):

\[ans = \min\limits_{i \in \mathbb{V}} (dp[\mathbb{V}][i] + dst(i, 0))\]

Запись \(\mathbb{V}\) обозначает множество всех вершин.

Может показаться, что порядок пересчёта такого ДП будет достаточно сложным. На самом деле это не так: заметьте что для пересчета \(dp[mask][i]\) нам нужно, чтобы уже был посчитан ответ для маски \(mask \backslash i\). Можно легко доказать, что в численном выражении \(mask \backslash i\) будет гарантированно меньше \(mask\), так как на некоторой позиции в \(mask\) будет находиться бит \(1\), а в \(mask \backslash i\) бит \(0\). Значит, можно просто пересчитывать ДП в порядке возрастания значения \(mask\) в численном выражении.

Реализация решения задачи о коммивояжёре

#include <bits/stdc++.h>

using namespace std;

const double INF = 1e9 + 7;     //бесконечность

double x[20], y[20];    //координаты городов.

//Заметим, что для N элементов существует 2^N возможных подмножеств (масок)
//значением от 0 до 2^N - 1.
//Можно просто возвести 2 в произвольную степень с помощью битового сдвига:
//2^N = 1 << N
double dp[1 << 20][20];

//Расстояние между городами a и b
double dst(int a, int b) {
    double dx = x[a] - x[b], dy = y[a] - y[b];
    return sqrt(dx * dx + dy * dy);
}

int main() {
    int n;
    cin >> n;

    for (int i = 0; i < n; i++) {
        cin >> x[i] >> y[i];
    }

    for (int mask = 0; mask < (1 << n); mask++) {
        for (int i = 0; i < n; i++) {
            dp[mask][i] = INF;
        }
    }

    dp[1][0] = 0;   //Маска 1 содержит только нулевой элемент.

    for (int mask = 2; mask < (1 << n); mask++) {
        for (int i = 0; i < n; i++) {
            if ((mask >> i) & 1) {      //Если mask содержит i
                int mask_without_i = mask ^ (1 << i);

                for (int j = 0; j < n; j++) {
                    if (j != i && ((mask >> j) & 1)) {  //Если j != i и mask содержит j
                        dp[mask][i] = min(dp[mask][i], dp[mask_without_i][j] + dst(j, i));
                    }
                }
            }
        }
    }

    double ans = INF;
    int mask_all = (1 << n) - 1;  //маска, содержащая все элементы

    for (int i = 0; i < n; i++) {
        ans = min(ans, dp[mask_all][i] + dst(i, 0));
    }

    cout << ans << endl;
}